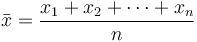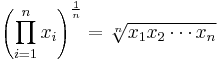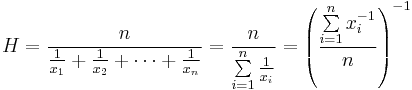Berarti vs. Median

- 3811
- 641
- Grant Zieme
Berarti (atau rata -rata) dan median adalah istilah statistik yang memiliki peran yang agak mirip dalam hal pemahaman kecenderungan sentral dari satu set skor statistik. Sementara rata-rata secara tradisional merupakan ukuran populer dari titik tengah dalam sampel, ia memiliki kelemahan yang dipengaruhi oleh nilai tunggal yang terlalu tinggi atau terlalu rendah dibandingkan dengan sisa sampel. Inilah sebabnya mengapa median kadang -kadang dianggap sebagai ukuran yang lebih baik dari titik tengah.
Grafik perbandingan
| Berarti | Median | |
|---|---|---|
| Definisi | Rata -rata adalah rata -rata aritmatika dari satu set angka, atau distribusi. Ini adalah ukuran yang paling umum digunakan dari kecenderungan sentral dari satu set angka. | Median digambarkan sebagai nilai numerik yang memisahkan bagian yang lebih tinggi dari sampel, populasi, atau distribusi probabilitas, dari bagian bawah. |
| Penerapan | Rata -rata digunakan untuk distribusi normal. | Median umumnya digunakan untuk distribusi miring. |
| Relevansi dengan kumpulan data | Meannya bukan alat yang kuat karena sebagian besar dipengaruhi oleh outlier. | Median lebih cocok untuk distribusi miring untuk mendapatkan pada kecenderungan sentral karena jauh lebih kuat dan masuk akal. |
| Cara menghitung | Rata -rata dihitung dengan menambahkan semua nilai dan membagi skor itu dengan jumlah nilai. | Median adalah angka yang ditemukan di tengah yang tepat dari himpunan nilai. Median dapat dihitung dengan mendaftarkan semua angka dalam urutan menaik dan kemudian menemukan angka di tengah distribusi tersebut. |
Definisi rata -rata dan median
Dalam matematika dan statistik, rata -rata atau rata -rata aritmatika dari daftar angka adalah jumlah dari seluruh daftar yang dibagi dengan jumlah item dalam daftar. Saat melihat distribusi simetris, rata -rata mungkin adalah ukuran terbaik untuk sampai pada kecenderungan sentral. Dalam teori dan statistik probabilitas, a median adalah jumlah itu yang memisahkan bagian yang lebih tinggi dari sampel, populasi, atau distribusi probabilitas, dari bagian bawah.
Cara menghitung
Itu Berarti atau rata -rata mungkin merupakan metode yang paling umum digunakan untuk menggambarkan kecenderungan sentral. Rata -rata dihitung dengan menambahkan semua nilai dan membagi skor itu dengan jumlah nilai. Itu rata -rata aritmatika sampel 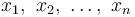 adalah jumlah nilai sampel dibagi dengan jumlah item dalam sampel:
adalah jumlah nilai sampel dibagi dengan jumlah item dalam sampel:
Itu Median adalah angka yang ditemukan di tengah yang tepat dari himpunan nilai. Median dapat dihitung dengan mendaftarkan semua angka dalam urutan menaik dan kemudian menemukan angka di tengah distribusi tersebut. Ini berlaku untuk daftar nomor ganjil; Dalam hal jumlah pengamatan yang merata, tidak ada nilai tengah tunggal, jadi itu adalah praktik yang biasa untuk mengambil rata -rata dari dua nilai tengah.
Contoh
Mari kita katakan bahwa ada sembilan siswa di kelas dengan skor berikut pada tes: 2, 4, 5, 7, 8, 10, 12, 13, 83. Dalam hal ini skor rata -rata (atau berarti) adalah jumlah dari semua skor yang dibagi sembilan. Ini berhasil hingga 144/9 = 16. Perhatikan bahwa meskipun 16 adalah rata -rata aritmatika, itu terdistorsi oleh skor 83 yang luar biasa tinggi dibandingkan dengan skor lain. Hampir semua skor siswa di bawah rata-rata. Oleh karena itu, dalam hal ini rata -rata bukanlah perwakilan yang baik dari kecenderungan sentral sampel ini.
Itu median, Di sisi lain, adalah nilai yang sedemikian rupa sehingga setengah dari skor di atasnya dan setengah dari skor di bawah ini. Jadi dalam contoh ini, mediannya adalah 8. Ada empat skor di bawah ini dan empat di atas nilai 8. Jadi 8 mewakili titik tengah atau kecenderungan sentral sampel.
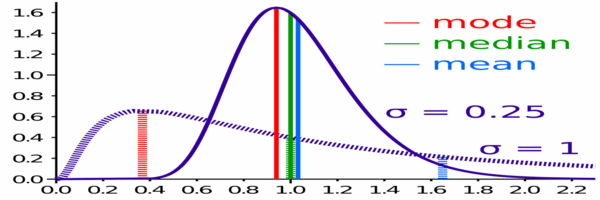 Perbandingan rata-rata, median dan mode dua distribusi log-normal dengan kemiringan yang berbeda.
Perbandingan rata-rata, median dan mode dua distribusi log-normal dengan kemiringan yang berbeda. Kerugian dari cara aritmatika dan median
Rata -rata bukanlah alat statistik yang kuat karena tidak dapat diterapkan pada semua distribusi tetapi dengan mudah merupakan alat statistik yang paling banyak digunakan untuk memperoleh kecenderungan pusat. Alasan bahwa rata -rata tidak dapat diterapkan pada semua distribusi adalah karena terlalu terpengaruh oleh nilai -nilai dalam sampel yang terlalu kecil hingga terlalu besar.
Kerugian median adalah sulit untuk menangani secara teoritis. Tidak ada formula matematika yang mudah untuk menghitung median.
Jenis cara lainnya
Ada banyak cara untuk menentukan kecenderungan sentral, atau rata -rata, dari serangkaian nilai. Rata -rata yang dibahas di atas secara teknis adalah rata -rata aritmatika, dan merupakan statistik yang paling umum digunakan untuk rata -rata. Ada jenis cara lain:
Rata -rata geometris
Rata -rata geometris didefinisikan sebagai Nakar produk dari N Angka, i.e., untuk satu set angka X1,X2,.. ,XN, rata -rata geometris didefinisikan sebagai
Cara geometris lebih baik daripada cara aritmatika untuk menggambarkan pertumbuhan proporsional. Misalnya, aplikasi yang baik untuk rata -rata geometris adalah menghitung tingkat pertumbuhan tahunan gabungan (CAGR).
Rata -rata harmonik
Rata -rata harmonik adalah timbal balik dari rata -rata aritmatika dari timbal balik. Rata -rata harmonik H dari bilangan real positif X1,X2,.. ,XN adalah
Aplikasi yang baik untuk sarana harmonik adalah saat rata -rata kelipatan. Untuk exampe, lebih baik menggunakan rata-rata harmonik tertimbang saat menghitung rasio harga rata-rata (P/E). Jika rasio P/E dirata -rata menggunakan rata -rata aritmatika tertimbang, titik data tinggi mendapatkan bobot yang terlalu besar daripada titik data rendah.
Berarti Pythagoras
Rata -rata aritmatika, rata -rata geometris dan rata -rata harmonik bersama -sama membentuk serangkaian cara yang disebut berarti Pythagoras. Untuk setiap set angka, rata -rata harmonik selalu merupakan yang terkecil dari semua cara Pythagoras, dan rata -rata aritmatika selalu yang terbesar dari 3 cara. Saya.e. Rata -rata harmonik ≤ rata -rata geometris ≤ rata -rata aritmatika.
Makna kata -kata lainnya
Berarti dapat digunakan sebagai figur ucapan dan memegang referensi sastra. Itu juga digunakan untuk menyiratkan miskin atau tidak hebat. Median, Dalam referensi geometris, adalah garis lurus yang melewati titik di segitiga ke tengah sisi yang berlawanan.