Perbedaan antara parabola dan hiperbola

Parabola vs hiperbola

Parabola dan hiperbola adalah dua bagian yang berbeda dari kerucut. Kita dapat menangani perbedaan mereka dalam penjelasan matematika atau menangani perbedaan dengan cara yang sangat sederhana yang tidak hanya matematikawan tetapi semua orang bisa mengerti. Artikel ini akan mencoba menjelaskan perbedaan di antara mereka dengan cara yang sangat sederhana.
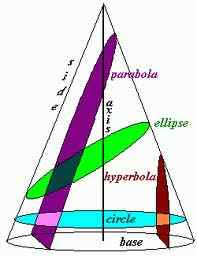
Pertama -tama, ketika sosok yang solid, yang dalam hal ini adalah kerucut, dipotong oleh pesawat, bagian yang diperoleh disebut bagian kerucut. Bagian kerucut bisa berupa lingkaran, elips, hiperbola, dan parabola tergantung pada sudut persimpangan antara sumbu kerucut dan bidang. Baik parabola dan hiperbola adalah kurva terbuka yang berarti bahwa lengan atau cabang kurva terus tak terbatas; Mereka bukan kurva tertutup seperti lingkaran atau elips.

Parabola
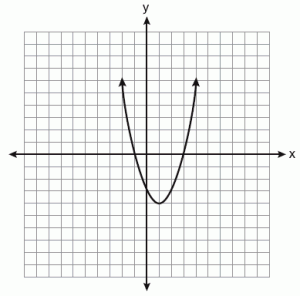
Parabola adalah kurva yang diperoleh ketika bidang memotong paralel dengan sisi kerucut. Dalam parabola, garis yang melewati fokus dan tegak lurus terhadap Directrix disebut "sumbu simetri."Ketika parabola berpotongan dengan titik pada" sumbu simetri, "itu disebut sebagai" verteks.“Semua parabola berbentuk identik karena dipotong pada sudut tertentu. Ini adalah ditandai oleh eksentrisitas “1.“Inilah alasan mengapa mereka semua bentuk yang sama tetapi dapat memiliki ukuran yang berbeda.

Parabola diberikan oleh persamaan y2 = x
Ketika satu set titik yang ada dalam bidang sama dengan Directrix, garis lurus yang diberikan, dan sama dari fokus, titik tertentu yang diperbaiki, itu disebut parabola.
Parabola memiliki banyak aplikasi praktis. Mereka digunakan untuk merancang jalur rudal, reflektor lampu mobil, teleskop, penerima radar, dan parabola satelit.

Hiperbola

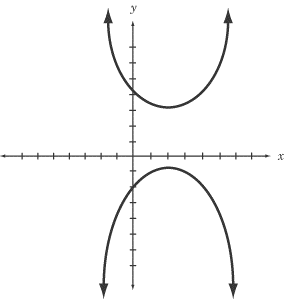
Hiperbola adalah kurva yang diperoleh ketika bidang memotong hampir sejajar dengan sumbu. Hiperbola tidak identik dalam bentuk karena ada banyak sudut antara sumbu dan bidang. "Vertices" adalah titik pada dua lengan yang paling dekat; Sedangkan segmen garis yang menghubungkan lengan disebut "sumbu utama."
Dalam parabola, kedua lengan kurva, juga disebut cabang, menjadi sejajar satu sama lain. Dalam hiperbola, kedua lengan atau kurva tidak menjadi paralel. Pusat Hyperbola adalah titik tengah dari sumbu utama.

Hiperbola diberikan oleh persamaan xy = 1

Ketika perbedaan jarak antara satu set titik yang ada dalam bidang ke dua fokus atau titik tetap adalah konstanta positif, itu disebut hiperbola.

Ringkasan:
Ketika satu set titik yang ada dalam bidang sama dengan Directrix, garis lurus yang diberikan, dan sama dari fokus, titik tertentu yang diperbaiki, itu disebut parabola. Ketika perbedaan jarak antara satu set titik yang ada dalam bidang ke dua fokus atau titik tetap adalah konstanta positif, itu disebut hiperbola.
Semua parabola memiliki bentuk yang sama tidak peduli berapa ukurannya; Semua hiperbola memiliki bentuk yang berbeda
Parabola diberikan oleh persamaan y2 = x; hiperbola diberikan oleh persamaan xy = 1
Dalam parabola kedua lengan menjadi sejajar satu sama lain sedangkan dalam hiperbola mereka tidak.