Perbedaan antara rata -rata dan median

- 3592
- 528
- Rodney Hegmann
 Kecenderungan sentral menyiratkan kecenderungan titik data untuk mengelompok di sekitar nilai pusat atau tengahnya. Dua ukuran kecenderungan sentral yang paling umum digunakan adalah rata -rata dan median. Berarti didefinisikan sebagai nilai 'pusat' dari set data yang diberikan sedangkan median adalah nilai 'paling tengah' dalam set data yang diberikan.
Kecenderungan sentral menyiratkan kecenderungan titik data untuk mengelompok di sekitar nilai pusat atau tengahnya. Dua ukuran kecenderungan sentral yang paling umum digunakan adalah rata -rata dan median. Berarti didefinisikan sebagai nilai 'pusat' dari set data yang diberikan sedangkan median adalah nilai 'paling tengah' dalam set data yang diberikan.
Ukuran yang ideal dari kecenderungan sentral adalah yang didefinisikan dengan jelas, mudah dipahami, hanya dapat dihitung. Itu harus didasarkan pada semua pengamatan dan paling tidak dipengaruhi oleh pengamatan ekstrem yang ada dalam set data.
Orang sering membandingkan dua langkah ini, tetapi faktanya mereka berbeda. Artikel ini secara khusus menyoroti perbedaan dasar antara rata -rata dan median. Lihat.
Konten: rata -rata vs median
- Grafik perbandingan
- Definisi
- Perbedaan utama
- Contoh
- Kesimpulan
Grafik perbandingan
| Dasar untuk perbandingan | Berarti | Median |
|---|---|---|
| Arti | Rata -rata mengacu pada rata -rata sederhana dari rangkaian nilai atau jumlah yang diberikan. | Median didefinisikan sebagai angka tengah dalam daftar nilai yang dipesan. |
| Apa itu? | Itu adalah rata -rata aritmatika. | Itu adalah rata -rata posisi. |
| Mewakili | Pusat gravitasi set data | Pusat gravitasi set data Titik tengah set data |
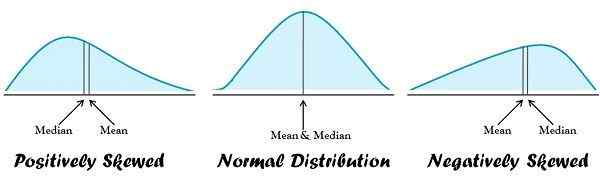
| Penerapan | Distribusi normal | Distribusi miring |
| Outlier | Mean sensitif terhadap outlier. | Median tidak sensitif terhadap outlier. |
| Perhitungan | Rata -rata dihitung dengan menambahkan semua pengamatan dan kemudian membagi nilai yang diperoleh dengan jumlah pengamatan. | Untuk menghitung median, kumpulan data diatur dalam urutan naik atau turun, maka nilai yang jatuh di tengah yang tepat dari set data baru, adalah median. |
Definisi rata -rata
Rata -rata adalah ukuran yang banyak digunakan dari kecenderungan sentral, yang didefinisikan sebagai rata -rata himpunan nilai. Ini mewakili model dan nilai paling umum dari kisaran nilai yang diberikan. Itu dapat dihitung, baik dalam seri diskrit dan kontinu.
Rata -rata sama dengan jumlah dari semua pengamatan yang dibagi dengan jumlah pengamatan dalam dataset. Jika nilai yang diasumsikan oleh variabel sama, rata -rata juga akan sama. Rata -rata dapat dari dua jenis, rata -rata sampel (x̅) dan rata -rata populasi (µ). Itu dapat dihitung dengan formula yang diberikan:
- Rata -rata aritmatika:
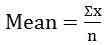 di mana ʃ = Surat Yunani Sigma, menunjukkan 'jumlah ...'
di mana ʃ = Surat Yunani Sigma, menunjukkan 'jumlah ...'
n = jumlah nilai - Untuk seri diskrit:
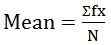 dimana, f = frekuensi
dimana, f = frekuensi - Untuk servis berkelanjutan:
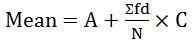 dimana d = (x-a)/c
dimana d = (x-a)/c
A = diasumsikan rata -rata
C = Pembagi Umum
Definisi median
Median adalah ukuran penting lain dari kecenderungan sentral, yang digunakan untuk membagi nilai menjadi dua bagian yang sama, i.e. setengah lebih besar dari sampel, populasi atau distribusi probabilitas dari bagian bawah. Itu adalah nilai paling tengah, yang dicapai ketika pengamatan diurutkan dalam urutan tertentu, baik menaik atau menurun pesanan.
Untuk perhitungan median, pertama -tama, atur pengamatan secara terendah ke tertinggi atau tertinggi ke terendah, kemudian oleskan formula yang sesuai, sesuai dengan kondisi diberikan di bawah ini:
- Jika jumlah pengamatannya aneh:
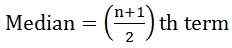 dimana n = jumlah pengamatan
dimana n = jumlah pengamatan - Jika jumlah pengamatan adalah bahkan:
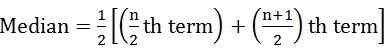
- Untuk seri berkelanjutan:
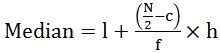 dimana, l = batas bawah kelas median
dimana, l = batas bawah kelas median
C = frekuensi kumulatif dari kelas median sebelumnya
f = frekuensi kelas median
h = lebar kelas
Perbedaan utama antara rata -rata dan median
Perbedaan signifikan antara rata -rata dan median disediakan dalam artikel yang diberikan di bawah ini:
- Dalam statistik, rata -rata didefinisikan sebagai rata -rata sederhana dari rangkaian nilai atau jumlah yang diberikan. Median dikatakan sebagai nomor tengah dalam daftar nilai yang dipesan.
- Sementara rata -rata adalah rata -rata aritmatika, median adalah rata -rata posisi, pada dasarnya, posisi set data menentukan nilai median.
- Rata-rata menguraikan pusat gravitasi set data sedangkan median menyoroti nilai paling tengah dari kumpulan data.
- Rata -rata sesuai untuk data yang didistribusikan secara normal. Di ujung lain, median adalah yang terbaik saat distribusi data condong.
- Rata -rata sangat dipengaruhi oleh nilai ekstrem yang tidak dalam kasus dengan median.
- Rata -rata dihitung dengan menambahkan semua pengamatan dan kemudian membagi nilai yang diperoleh dengan jumlah pengamatan; Hasilnya berarti. Berbeda dengan median, kumpulan data diatur dalam urutan naik atau turun, maka nilai yang jatuh di tengah yang tepat dari set data baru adalah median.
Contoh
Temukan rata -rata dan median dari set data yang diberikan:
58, 26, 65, 34, 78, 44, 96
Solusi: Untuk menghitung rata -rata, Anda perlu membagi jumlah pengamatan dengan jumlah pengamatan,
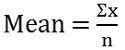
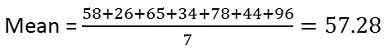 Rata -rata = 57.28
Rata -rata = 57.28
Untuk menghitung median, pertama -tama, atur seri dalam urutan, i.e. terendah ke tertinggi,
26, 34, 44, 58, 65, 78, 96
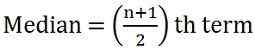 dimana n = jumlah pengamatan
dimana n = jumlah pengamatan
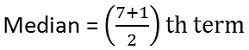 Median = 4th Istilah = 58
Median = 4th Istilah = 58
Kesimpulan
Setelah meninjau poin -poin di atas, kita dapat mengatakan bahwa kedua konsep matematika ini berbeda. Rerata atau rata -rata aritmatika dianggap sebagai ukuran terbaik dari kecenderungan sentral karena mengandung semua fitur dari ukuran yang ideal tetapi memiliki satu kelemahan bahwa fluktuasi pengambilan sampel mempengaruhi rata -rata.
Dengan cara yang sama, median juga jelas didefinisikan dan mudah dipahami dan dihitung, dan hal terbaik tentang ukuran ini adalah bahwa itu tidak terpengaruh oleh fluktuasi pengambilan sampel, tetapi satu -satunya kelemahan dari median adalah bahwa itu tidak didasarkan pada semua pada semua Pengamatan. Untuk klasifikasi ujung terbuka, median biasanya lebih disukai daripada rata -rata.

