Perbedaan antara dispersi dan kemiringan

Tingkat variasi sering diekspresikan dalam hal data numerik untuk tujuan perbandingan satu -satunya dalam teori dan analisis statistik. Kami biasanya menghitung satu angka untuk mewakili seluruh rangkaian data, yang disebut "rata -rata". Namun, itu tidak menentukan cara tertentu untuk menentukan komposisi seri. Karena itu, langkah -langkah tambahan diperlukan untuk mencerahkan kita tentang bagaimana item bervariasi satu sama lain atau di sekitar rata -rata. Untuk memahami banyak konsep analisis kuantitatif dalam statistik, kami menggunakan ukuran dispersi dan kemiringan. Dispersi adalah ukuran rentang distribusi di sekitar lokasi pusat sedangkan kemiringan adalah ukuran asimetri dalam distribusi statistik.

Apa itu dispersi?

Dalam statistik, dispersi adalah ukuran bagaimana mendistribusikan data berarti itu menentukan bagaimana nilai -nilai dalam set data berbeda satu sama lain dalam ukuran. Ini adalah kisaran di mana distribusi statistik tersebar di sekitar titik pusat. Ini terutama menentukan variabilitas item data yang ditetapkan di sekitar titik pusatnya. Sederhananya, ini mengukur tingkat variabilitas di sekitar nilai rata -rata. Ukuran dispersi penting untuk menentukan penyebaran data di sekitar ukuran lokasi. Misalnya, varian adalah ukuran standar dispersi yang menentukan bagaimana data didistribusikan tentang rata -rata. Ukuran dispersi lainnya adalah kisaran dan deviasi rata -rata.

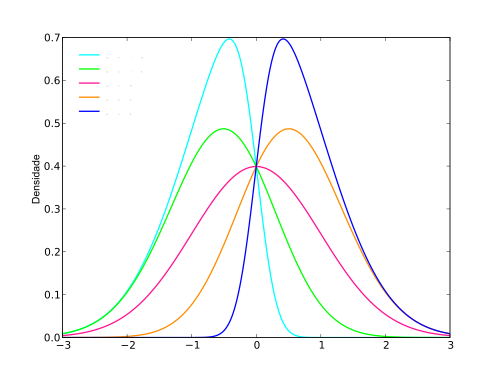
Apa itu kemiringan?

Kemiringan adalah ukuran asimetri distribusi tentang titik tertentu. Distribusi mungkin sedikit asimetris, sangat asimetris, atau simetris. Ukuran asimetri distribusi dihitung menggunakan kemiringan. Dalam hal kemiringan positif, distribusi dikatakan jejak kanan dan ketika kemiringannya negatif, distribusi dikatakan matang kiri. Jika kemiringannya nol, distribusinya simetris. Kecenderungan diukur berdasarkan rata -rata, median, dan mode. Nilai kemiringan bisa positif, negatif, atau tidak terdefinisi tergantung pada apakah titik data condong ke kiri, atau condong ke kanan.

Perbedaan antara dispersi dan kemiringan

1. Definisi dispersi vs. Kecondongan

Dalam istilah statistik dan teori probabilitas, dispersi adalah ukuran kisaran nilai untuk variabel acak atau distribusi probabilitasnya. Ini menggambarkan rentang yang distribusi di mana suatu distribusi diregangkan atau disebarkan. Sederhananya, ini adalah ukuran untuk mempelajari variabilitas item. Skewness, di sisi lain, adalah ukuran asimetri dalam distribusi statistik variabel acak tentang rata -rata. Nilai kemiringan bisa positif dan negatif, atau terkadang tidak terdefinisi. Sederhananya, distribusi asimetris dikatakan miring

2. Ukuran dispersi vs. Kecondongan

Ukuran dispersi berarti sejauh mana variasi tidak seimbang dari nilai pusatnya. Lebih tepatnya, ini mengukur tingkat variabilitas dalam nilai variabel di sekitar nilai rata -rata. Dispersi menunjukkan penyebaran data. Ukuran kemiringan berarti bagaimana asimetris distribusi dan menentukan apakah titik data condong ke kanan atau ke kiri. Jika distribusinya dikatakan condong ke kiri, maka nilainya negatif dan nilainya positif jika distribusinya condong ke kanan.

3. Perhitungan dispersi vs. Kecondongan

Dispersi dihitung berdasarkan rata -rata tertentu. Ini adalah perhitungan statistik yang mengukur tingkat variasi dan ada banyak cara berbeda untuk menghitung dispersi, tetapi dua yang paling umum adalah kisaran dan deviasi rata -rata. Rentang adalah perbedaan antara nilai terbesar dan terkecil dalam satu set data, sedangkan deviasi rata -rata adalah rata -rata nilai absolut dari penyimpangan nilai fungsional dari titik pusat. Skewness, di sisi lain, dihitung berdasarkan rata -rata, median, dan mode. Jika rata -rata lebih besar dari mode, Anda memiliki kemiringan positif dan jika rata -rata kurang dari mode, Anda memiliki kemiringan negatif. Selain itu, distribusi memiliki nol condong jika terjadi distribusi simetris.

4. Aplikasi dispersi vs. Kecondongan

Dispersi terutama digunakan untuk menggambarkan hubungan antara satu set data dan menentukan tingkat variasi nilai data dari nilai rata -rata mereka. Dispersi statistik dapat digunakan untuk metode statistik lainnya seperti analisis regresi, yang merupakan proses yang digunakan untuk memahami hubungan antara variabel. Itu juga dapat digunakan untuk menguji reliabilitas rata -rata. Skewness, di sisi lain, berurusan dengan sifat distribusi dalam satu set data. Sangat membantu dalam hal analisis ekonomis di sektor keuangan yang melibatkan serangkaian data besar seperti pengembalian aset, harga saham, dll.

Dispersi vs. Skewness: Bagan Perbandingan

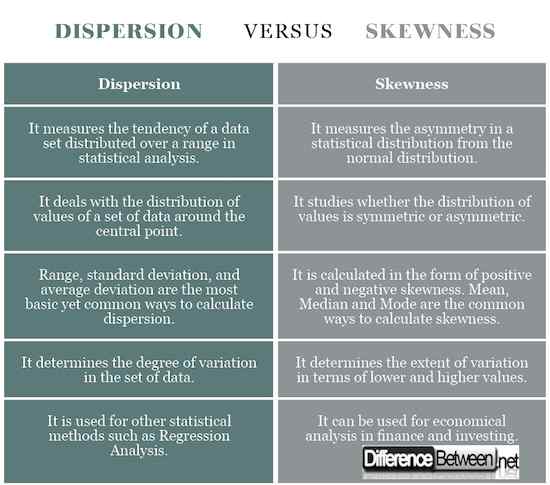
Ringkasan dispersi vs. Kecondongan

Keduanya adalah istilah yang paling umum digunakan dalam analisis statistik dan teori probabilitas untuk mengkarakterisasi kumpulan data yang melibatkan sejumlah besar data numerik. Dispersi adalah ukuran untuk menghitung variabilitas dalam data atau untuk mempelajari variasi data di antara mereka sendiri atau di sekitar rata -rata. Ini terutama berkaitan dengan distribusi nilai data dalam satu set di sekitar titik pusatnya. Ini dapat diukur dalam beberapa cara, dari mana kisaran dan deviasi rata -rata adalah yang paling umum. Kemiringan digunakan untuk mengukur asimetri dari distribusi normal dalam set data yang berarti sejauh mana distribusi tidak seimbang di sekitar rata-rata.