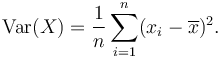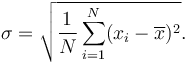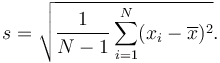Standar deviasi vs. Perbedaan
- 4874
- 1280
- Marion Hegmann
Deviasi standar Dan perbedaan adalah ukuran statistik dispersi data, i.e., Mereka mewakili berapa banyak variasi yang ada dari rata -rata, atau sejauh mana nilai -nilai biasanya "menyimpang" dari rata -rata (rata -rata). Varians atau standar deviasi nol menunjukkan bahwa semua nilai identik.
Varians adalah rata -rata kotak penyimpangan (i.e., perbedaan nilai dari rata -rata), dan standar deviasi adalah akar kuadrat dari varian itu. Deviasi standar digunakan untuk mengidentifikasi outlier dalam data.
Grafik perbandingan
Perbedaan - Persamaan -| Deviasi standar | Perbedaan | |
|---|---|---|
| Formula Matematika | Akar varians kuadrat | Rata -rata kotak penyimpangan masing -masing nilai dari rata -rata dalam sampel. |
| Simbol | Surat Yunani Sigma - σ | Tidak ada simbol khusus; dinyatakan dalam hal standar deviasi atau nilai lainnya. |
| Nilai dalam kaitannya dengan kumpulan data yang diberikan | Skala yang sama dengan nilai dalam set data yang diberikan; Oleh karena itu, dinyatakan dalam unit yang sama. | Skala lebih besar dari nilai dalam set data yang diberikan; tidak dinyatakan dalam unit yang sama dengan nilai itu sendiri. |
| Adalah nilai negatif atau positif? | Selalu tidak negatif | Selalu tidak negatif |
| Aplikasi Dunia Nyata | Pengambilan sampel populasi; mengidentifikasi outlier | Rumus statistik, keuangan. |
Konsep penting
- Berarti: Rata -rata semua nilai dalam set data (tambahkan semua nilai dan membagi jumlahnya dengan jumlah nilai).
- Deviasi: jarak masing -masing nilai dari rata -rata. Jika rata -rata adalah 3, nilai 5 memiliki penyimpangan 2 (kurangi rata -rata dari nilai). Penyimpangan bisa positif atau negatif.
Simbol
Rumus untuk standar deviasi dan varian sering diekspresikan menggunakan:
- x̅ = rata -rata, atau rata -rata, dari semua titik data dalam masalah
- X = titik data individu
- N = jumlah titik dalam set data
- ∑ = jumlah [kotak penyimpangan]
Rumus
Varian satu set N Nilai yang sama -sama mungkin dapat ditulis sebagai:
Deviasi standar adalah akar kuadrat dari varian:
Rumus dengan huruf -huruf Yunani memiliki cara untuk terlihat menakutkan, tetapi ini kurang rumit dari yang terlihat. Untuk meletakkannya dalam langkah sederhana:
- Temukan rata -rata semua titik data
- Cari tahu seberapa jauh setiap titik jauh dari rata -rata (ini adalah penyimpangan)
- persegi setiap penyimpangan (i.e. perbedaan setiap nilai dari rata -rata)
- Bagilah jumlah kotak dengan jumlah poin.
Yang memberikan varian. Ambil akar kuadrat dari varian untuk menemukan standar deviasi.
Video luar biasa ini dari Khan Academy menjelaskan konsep varians dan standar deviasi:
Contoh
Katakanlah set data termasuk ketinggian enam dandelion: 3 inci, 4 inci, 5 inci, 4 inci, 11 inci, dan 6 inci.
Pertama, temukan rata -rata titik data: (3 + 4 + 5 + 4 + 11 + 7) / 6 = 5.5
Jadi tinggi rata -rata adalah 5.5 inci. Sekarang kita membutuhkan penyimpangan, jadi kita menemukan perbedaan setiap tanaman dari rata -rata: -2.5, -1.5, -.5, -1.5, 5.5, 1.5
Sekarang persegi setiap penyimpangan dan temukan jumlah mereka: 6.25 + 2.25 + .25 + 2.25 + 30.25 + 2.25 = 43.5
Sekarang bagi jumlah kotak dengan jumlah titik data, dalam hal ini tanaman: 43.5/6 = 7.25
Jadi varian dari set data ini adalah 7.25, yang merupakan angka yang cukup sewenang -wenang. Untuk mengubahnya menjadi pengukuran dunia nyata, ambil akar kuadrat 7.25 untuk menemukan standar deviasi dalam inci.
Deviasi standar sekitar 2.69 inci. Itu berarti bahwa untuk sampel, setiap dandelion dalam 2.69 inci rata -rata (5.5 inci) adalah 'normal'.
Mengapa menyimpulkan penyimpangan?
Penyimpangan dikuadratkan untuk mencegah nilai negatif (penyimpangan di bawah rata -rata) membatalkan nilai positif. Ini berfungsi karena angka negatif kuadrat menjadi nilai positif. Jika Anda memiliki set data sederhana dengan penyimpangan dari rata -rata +5, +2, -1, dan -6, jumlah penyimpangan akan keluar sebagai nol jika nilainya tidak dikuadratkan (i.e. 5 + 2 - 1 - 6 = 0).
Aplikasi Dunia Nyata
Varians dinyatakan sebagai dispersi matematika. Karena ini adalah angka yang sewenang-wenang relatif terhadap pengukuran asli dari set data, sulit untuk memvisualisasikan dan berlaku dalam arti dunia nyata. Menemukan varian biasanya hanya langkah terakhir sebelum menemukan standar deviasi. Nilai varians kadang -kadang digunakan dalam formula keuangan dan statistik.
Deviasi standar, yang dinyatakan dalam unit asli dari set data, jauh lebih intuitif dan lebih dekat dengan nilai -nilai set data asli. Paling sering digunakan untuk menganalisis demografi atau sampel populasi untuk mendapatkan rasa apa yang normal dalam populasi.
Menemukan outlier
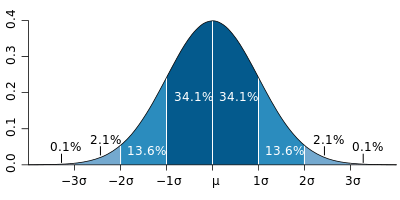Distribusi normal (kurva lonceng) dengan pita yang sesuai dengan 1σ Dalam distribusi normal, sekitar 68% dari populasi (atau nilai) termasuk dalam 1 standar deviasi (1σ) dari rata -rata dan sekitar 94% jatuh dalam 2σ. Nilai yang berbeda dari rata -rata dengan 1.7σ atau lebih biasanya dianggap outlier.
Dalam praktiknya, sistem kualitas seperti enam sigma berupaya mengurangi tingkat kesalahan sehingga kesalahan menjadi outlier. Istilah "Proses Six Sigma" berasal dari gagasan bahwa jika seseorang memiliki enam standar deviasi antara rata -rata proses dan batas spesifikasi terdekat, praktis tidak ada item yang gagal memenuhi spesifikasi.[1]
Sampel standar deviasi
Di aplikasi dunia nyata, set data yang digunakan biasanya mewakili sampel populasi, bukan seluruh populasi. Formula yang sedikit dimodifikasi digunakan jika kesimpulan seluruh populasi harus diambil dari sampel parsial.
'Sampel standar deviasi' digunakan jika yang Anda miliki adalah sampel, tetapi Anda ingin membuat pernyataan tentang standar deviasi populasi dari mana sampel diambil
Satu-satunya cara sampel formula standar deviasi berbeda dari rumus standar deviasi adalah "-1" dalam penyebut.
Dengan menggunakan contoh dandelion, formula ini akan diperlukan jika kami mencicipi hanya 6 dandelion, tetapi ingin menggunakan sampel itu untuk menyatakan standar deviasi untuk seluruh bidang dengan ratusan dandelion.
Jumlah kotak sekarang akan dibagi dengan 5 bukan 6 (n - 1), yang memberikan varian 8.7 (bukan 7.25), dan sampel standar deviasi 2.95 inci, bukan 2.69 inci untuk standar deviasi asli. Perubahan ini digunakan untuk menemukan margin kesalahan dalam sampel (9% dalam kasus ini).