Perbedaan antara asimptot horizontal dan vertikal

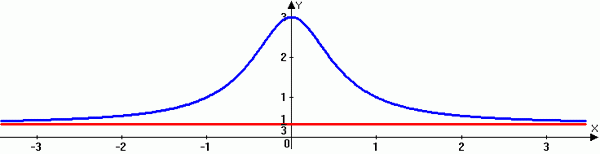
Sebelum kita masuk ke topik asimptot horizontal dan vertikal, mari kita coba memahami apa sebenarnya asimtot dan peran apa yang mereka mainkan dalam matematika. Dalam geometri proyektif, asimptot adalah garis lurus yang mendekati kurva yang diberikan secara sewenang -wenang tetapi tidak bertemu pada jarak yang terbatas. Secara geometris, garis adalah asimptot dari kurva y = f (x), jika jarak antara garis dan titik 'p' pada kurva mendekati nol karena x dan y keduanya cenderung tak terbatas. Grafik dapat memiliki satu asimptot yang sejajar dengan setiap sumbu. Sebenarnya, asimptot adalah sesuatu yang tidak ada secara fisik - ini lebih seperti khayalan.

Asimptot membantu menentukan tindakan atau bentuk hal -hal, tetapi itu sebenarnya bukan bagian dari grafik. Ini hanyalah garis imajiner yang membantu Anda membuat grafik fungsi rasional. Saat kurva mendekati ke arah asimptot, ia semakin dekat dan lebih dekat ke asimtot tetapi tidak pernah benar -benar menyentuhnya. Dengan demikian, asimptot membantu menentukan di mana grafik fungsi dapat atau tidak bisa pergi. Yang sedang berkata, ada tiga jenis asimptot: asimtot vertikal, horizontal dan miring. Tapi kita hanya akan membahas asimtot vertikal dan asimtot horizontal, dan melihat bagaimana mencari tahu yang sebenarnya.

Apa itu asimptot horizontal?

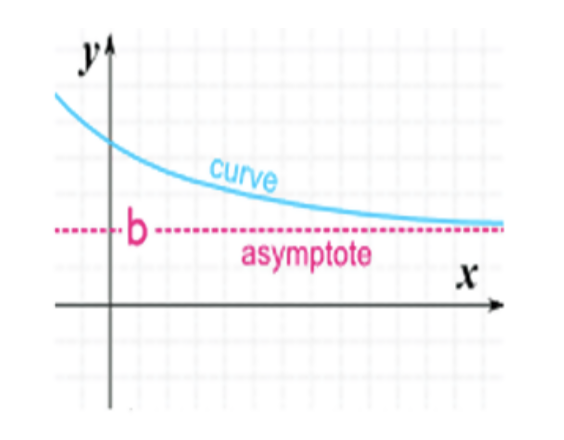
Asimptot horizontal adalah nilai konstan pada grafik yang didekati fungsi tetapi tidak benar -benar mencapai. Itu menunjukkan apa yang sebenarnya terjadi pada kurva saat nilai-X menjadi sangat besar atau sangat kecil. Dalam contoh grafis di atas, kurva mendekati nilai konstan B, tetapi tidak pernah benar -benar mencapai, y = 0.

Baris y = b adalah asimptot horizontal dari grafik 'f' jika f (x) -> b sebagai x -> ∞ atau x -> -∞

Untuk menemukan asimptot horizontal dari fungsi rasional, tingkat polinomial dalam pembilang dan penyebut harus dipertimbangkan.

• Jika penyebut memiliki daya variabel tertinggi dalam persamaan fungsi, asimptot horizontal secara otomatis sumbu x atau y = 0.
• Jika pembilang dan penyebut memiliki tingkat yang sama, ambil koefisien utama dari istilah -istilah tersebut dengan kekuatan tertinggi dan buat sebagian kecil dari mereka untuk menemukan asimptot horizontal
• Jika pembilang memiliki daya variabel tertinggi dalam persamaan fungsi, fungsi tidak memiliki asimptot horizontal; Grafik mungkin akan memiliki asimptot miring.

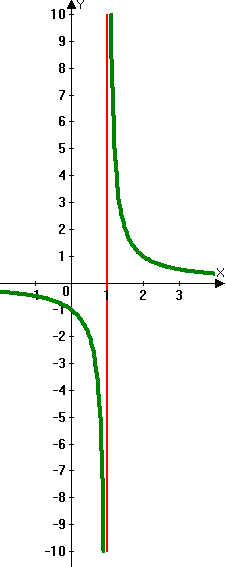
Apa itu asimptot vertikal?

Karena penyebut fraksi tidak akan pernah nol, memiliki variabel di bagian bawah jika fraksi bisa menjadi masalah. Beberapa nilai domain 'x' membuat penyebut nol dan fungsi akan melompati nilai ini dalam grafik, membuat asimptot vertikal. Mereka adalah garis vertikal yang ditarik dengan ringan atau dengan tanda hubung untuk menunjukkan bahwa mereka bukan bagian dari grafik.

Jika bilangan real 'a' adalah nol dari denominator q (x), maka grafik f (x) = p (x)/q (x), di mana p (x) dan q (x) tidak memiliki umum umum faktor, memiliki asimptot vertikal, x = a.

Perbedaan antara asimptot horizontal dan vertikal

Definisi

- Asimptot horizontal adalah nilai konstan pada grafik yang didekati fungsi tetapi tidak benar -benar mencapai. Itu menunjukkan apa yang sebenarnya terjadi pada kurva saat nilai-X menjadi sangat besar atau sangat kecil. Asimtot vertikal, di sisi lain, adalah garis vertikal yang tidak terlihat yang sesuai dengan nol dalam penyebut fraksi rasional. Mereka adalah garis vertikal yang ditarik dengan ringan atau dengan tanda hubung untuk menunjukkan bahwa mereka bukan bagian dari grafik.

Perhitungan

- Untuk menentukan asimptot horizontal dari fungsi rasional, tingkat polinomial dalam pembilang dan penyebut harus dipertimbangkan. Jika penyebut memiliki daya variabel tertinggi dalam persamaan fungsi, asimptot horizontal secara otomatis sumbu x atau y = 0. Jika kedua pembilang dan penyebut memiliki derajat yang sama, maka buat sebagian kecil dari koefisiennya untuk menentukan persamaan asimptot horizontal. Untuk menentukan asimtot vertikal dari fungsi rasional, atur denominator fraksi sama dengan nol.

Contoh

- Mari kita temukan asimtot fungsi

Y = 3x²+9x-21 ∕ x²-25

Untuk menemukan asimtot vertikal, atur denominator fraksi sama dengan nol.

X²-25 = 0

(x-5) (x+5) = 0

x = 5 dan x = - 5

Dua angka ini adalah dua nilai yang tidak dapat dimasukkan dalam domain, jadi persamaannya adalah asimtot vertikal. Jadi, dua asimtot vertikal adalah, x = 5 dan x = - 5.

Sekarang, untuk menentukan asimptot horizontal, lihat persamaan aslinya. Di sini, daya variabel tertinggi adalah 2. Karena pembilang dan penyebut memiliki tingkat kekuatan yang sama, buat sebagian kecil dari koefisien mereka:

y = 3x²/X²

y = 3/1

y = 3

Jadi, persamaan asimptot horizontal adalah, y = 3.

Asimptot horizontal vs. Asimptot vertikal: Bagan perbandingan

Ringkasan Asimptot Horizontal VS. Asimptot vertikal

Asimptot membantu menentukan tindakan atau bentuk hal -hal, tetapi itu sebenarnya bukan bagian dari grafik. Asimtot vertikal menandai tempat di mana fungsi tidak memiliki domain. Anda memecahkan persamaan asimtot vertikal dengan mengatur denominator fraksi sama dengan nol. Asimtot horizontal, di sisi lain, menunjukkan apa yang terjadi pada kurva saat nilai-X menjadi sangat besar atau sangat kecil. Untuk menemukan asimptot horizontal, Anda perlu mempertimbangkan tingkat polinomial dalam pembilang dan penyebutnya.