Perbedaan antara diferensial dan turunan

Untuk lebih memahami perbedaan antara diferensial dan turunan dari suatu fungsi, Anda perlu memahami konsep fungsi terlebih dahulu.

Fungsi adalah salah satu konsep dasar dalam matematika yang mendefinisikan hubungan antara satu set input dan satu set output yang mungkin terjadi di mana setiap input terkait dengan satu output. Salah satu variabel adalah variabel independen dan variabel lainnya adalah variabel dependen.

Konsep fungsi adalah salah satu topik yang paling diremehkan dalam matematika tetapi sangat penting dalam mendefinisikan hubungan fisik. Ambil contoh: Pernyataan "y adalah fungsi x" berarti sesuatu yang terkait dengan y terkait langsung dengan x oleh beberapa formula. Katakanlah jika inputnya 6 dan fungsinya adalah menambahkan 5 ke input 6. Hasilnya adalah 6+5 = 11, yang merupakan output Anda.

Ada beberapa pengecualian dalam matematika atau Anda dapat mengatakan masalah, yang tidak dapat diselesaikan dengan metode geometri dan aljabar biasa saja. Cabang baru matematika yang dikenal sebagai kalkulus digunakan untuk menyelesaikan masalah ini.

Kalkulus pada dasarnya berbeda dari matematika yang tidak hanya menggunakan ide -ide dari geometri, aritmatika, dan aljabar, tetapi juga berkaitan dengan perubahan dan gerakan.

Kalkulus sebagai alat mendefinisikan turunan dari suatu fungsi sebagai batas jenis tertentu. Konsep turunan dari suatu fungsi membedakan kalkulus dari cabang matematika lainnya. Diferensial adalah subbidang kalkulus yang mengacu pada perbedaan yang sangat kecil dalam beberapa kuantitas yang bervariasi dan merupakan salah satu dari dua divisi dasar kalkulus. Cabang lain disebut Kalkulus Integral.

Apa itu diferensial?

Diferensial adalah salah satu divisi fundamental kalkulus, bersama dengan kalkulus integral. Ini adalah subbidang kalkulus yang berkaitan dengan perubahan yang sangat kecil dalam beberapa kuantitas yang berbeda -beda. Dunia tempat kita tinggal penuh dengan jumlah yang saling terkait yang berubah secara berkala.

Misalnya, luas badan melingkar yang berubah saat jari -jari berubah atau proyektil yang berubah dengan kecepatan. Entitas yang berubah ini, dalam istilah matematika, disebut sebagai variabel dan laju perubahan satu variabel sehubungan dengan yang lain adalah turunan. Dan persamaan yang mewakili hubungan antara variabel -variabel ini disebut persamaan diferensial.

Persamaan diferensial adalah persamaan yang berisi fungsi yang tidak diketahui dan beberapa turunannya.

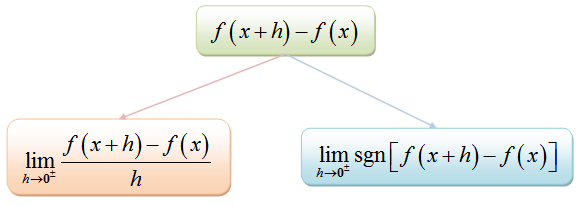
Apa turunannya?

Konsep turunan dari suatu fungsi adalah salah satu konsep paling kuat dalam matematika. Turunan fungsi biasanya merupakan fungsi baru yang disebut sebagai fungsi turunan atau fungsi laju.

Turunan fungsi mewakili laju perubahan instan dalam nilai variabel dependen sehubungan dengan perubahan nilai variabel independen. Ini adalah alat fundamental kalkulus yang juga dapat diartikan sebagai kemiringan garis garis singgung. Ini mengukur seberapa curam grafik suatu fungsi pada beberapa titik yang diberikan pada grafik.

Secara sederhana, turunan adalah tingkat di mana fungsi berubah pada titik tertentu.

Perbedaan antara diferensial dan turunan

Definisi diferensial VS. Turunan

Kedua istilah diferensial dan turunan terhubung secara erat satu sama lain dalam hal hubungan timbal balik. Dalam matematika yang berubah, entitas disebut variabel dan laju perubahan satu variabel sehubungan dengan yang lain disebut sebagai turunan.

Persamaan yang mendefinisikan hubungan antara variabel -variabel ini dan turunannya disebut persamaan diferensial. Diferensiasi adalah proses menemukan turunan. Turunan fungsi adalah laju perubahan nilai output sehubungan dengan nilai inputnya, sedangkan diferensial adalah perubahan aktual fungsi.

Hubungan diferensial VS. Turunan

Diferensiasi adalah metode menghitung turunan yang merupakan laju perubahan output y dari fungsi sehubungan dengan perubahan variabel x.

Secara sederhana, turunan mengacu pada laju perubahan y sehubungan dengan x, dan hubungan ini dinyatakan sebagai y = f (x), yang berarti y adalah fungsi dari x. Turunan fungsi f (x) didefinisikan sebagai fungsi yang nilainya menghasilkan kemiringan f (x) di mana ia didefinisikan dan f (x) dapat dibedakan. Itu mengacu pada kemiringan grafik pada titik tertentu.

Representasi diferensial VS. Turunan

Perbedaan direpresentasikan sebagai DX, Dy, Dt, dan seterusnya, dimana Dx mewakili perubahan kecil dalam x, Dy mewakili perubahan kecil dalam y, dan Dt adalah perubahan kecil dalam t. Saat membandingkan perubahan dalam jumlah terkait di mana y adalah fungsi x, diferensial Dy dapat ditulis sebagai:

Dy = f^'(X) DX

Turunan dari suatu fungsi adalah kemiringan fungsi pada titik mana pun dan ditulis sebagai D/DX. Misalnya, turunan dosa (x) dapat ditulis sebagai:

D/Dx sin (x) = sin (x)^' = cos (x)

Diferensial vs. Derivatif: Bagan Perbandingan

Ringkasan diferensial VS. Turunan

Dalam matematika, laju perubahan satu variabel sehubungan dengan variabel lain disebut turunan dan persamaan yang mengekspresikan hubungan antara variabel -variabel ini dan turunannya disebut persamaan diferensial. Singkatnya, persamaan diferensia melibatkan turunan yang sebenarnya menentukan bagaimana kuantitas berubah sehubungan dengan yang lain. Dengan memecahkan persamaan diferensial, Anda mendapatkan formula untuk jumlah yang tidak mengandung turunan. Metode menghitung turunan disebut diferensiasi. Secara sederhana, turunan dari suatu fungsi adalah laju perubahan nilai output sehubungan dengan nilai inputnya, sedangkan diferensial adalah perubahan fungsi aktual.