Perbedaan antara integral yang pasti dan tidak terbatas

Kalkulus adalah cabang penting dari matematika, dan diferensiasi memainkan peran penting dalam kalkulus. Proses terbalik dari diferensiasi dikenal sebagai integrasi, dan terbalik dikenal sebagai integral, atau sedemikian rupa, kebalikan dari diferensiasi memberikan integral. Berdasarkan hasil mereka menghasilkan integral dibagi menjadi dua kelas yaitu., integral yang pasti dan tidak terbatas.

Integral yang pasti

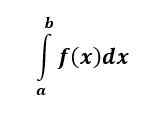
Integral yang pasti f (x) adalah angka dan mewakili area di bawah kurva f (x) dari x = a ke x = b.

Integral yang pasti memiliki batas atas dan bawah pada integral, dan itu disebut pasti karena, pada akhir masalah, kami memiliki angka - itu adalah jawaban yang pasti.

Integral yang tidak terbatas

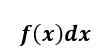
Integral yang tidak terbatas dari f (x) adalah fungsi dan menjawab pertanyaan, “Fungsi apa yang dibedakan f (x)?"

Dengan integral yang tidak terbatas, tidak ada batasan atas dan bawah pada integral di sini, dan apa yang akan kita dapatkan adalah jawaban yang masih ada Xdi dalamnya dan juga akan memiliki konstan (biasanya dilambangkan dengan C) di dalamnya.

Integral yang tidak terbatas biasanya memberikan solusi umum untuk persamaan diferensial.

Integral yang tidak terbatas lebih merupakan bentuk integrasi umum, dan dapat ditafsirkan sebagai anti-derivatif dari fungsi yang dipertimbangkan.

Misalkan diferensiasi fungsi F mengarah ke fungsi lain F, dan integrasi f memberikan integral. Secara simbolis, ini ditulis sebagai

F (x) = ∫ƒ (x) dx

atau

F = ∫ƒ dx

dimana keduanya F Dan ƒ adalah fungsi X, Dan F berbeda. Dalam bentuk di atas, ini disebut reimann integral dan fungsi yang dihasilkan menyertai konstanta sewenang -wenang.

Integral yang tidak terbatas sering menghasilkan keluarga fungsi; Oleh karena itu, integral tidak terbatas.

Integral dan proses integrasi adalah jantung dari pemecahan persamaan diferensial. Namun, tidak seperti langkah -langkah dalam diferensiasi, langkah -langkah dalam integrasi tidak selalu mengikuti rutin yang jelas dan standar. Kadang -kadang, kita melihat bahwa solusi tidak dapat diekspresikan secara eksplisit dalam hal fungsi dasar. Dalam hal ini, solusi analitik sering diberikan dalam bentuk integral yang tidak terbatas.

Teorema Kalkulus mendasar

Yang pasti dan integral tidak terbatas dihubungkan oleh teorema fundamental kalkulus sebagai berikut: untuk menghitung a integral yang pasti, temukan Integral yang tidak terbatas (juga dikenal sebagai anti-turunan) dari fungsi dan mengevaluasi pada titik akhir x = a Dan x = b.

Perbedaan antara integral yang pasti dan tidak terbatas akan terbukti begitu kita mengevaluasi integral untuk fungsi yang sama.

Pertimbangkan integral berikut:

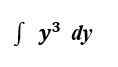
OKE. Mari kita lakukan keduanya dan lihat perbedaannya.

Untuk integrasi, kita perlu menambahkan satu ke indeks yang membawa kita ke ekspresi berikut:

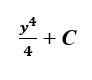
Pada titik waktu ini C hanyalah konstan bagi kita. Informasi tambahan diperlukan dalam masalah untuk menentukan nilai yang tepat C.

Mari kita evaluasi integral yang sama dalam bentuknya yang pasti.e., dengan batas atas dan bawah termasuk.

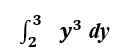
Secara grafis, kami sekarang menghitung area di bawah kurva f (x) = y³ di antara y = 2 Dan y = 3.

Langkah pertama dalam evaluasi ini sama dengan evaluasi integral yang tidak terbatas. Satu -satunya perbedaan adalah bahwa kali ini kita tidak menambahkan konstan C.

Ekspresi dalam kasus ini terlihat sebagai berikut:

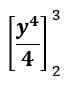
Ini adalah giliran ke arah:

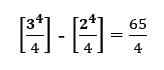
Pada dasarnya, kami menggantikan 3 dan kemudian 2 dalam ekspresi dan memperoleh perbedaan di antara mereka.

Ini adalah nilai pasti yang bertentangan dengan penggunaan konstan C lebih awal.

Mari kita jelajahi faktor konstan (sehubungan dengan integral yang tidak terbatas) dalam beberapa detail lebih lanjut.

Jika diferensial y³ adalah 3y², Kemudian

∫3y²dy = y³

Namun, 3y² bisa menjadi perbedaan dari banyak ekspresi yang beberapa di antaranya termasuk y³-5, y³+7, dll ... ini menyiratkan bahwa pembalikan tidak unik karena konstan tidak terhitung selama operasi.

Jadi secara umum, 3y² adalah perbedaan y³+C Di mana C ada konstan. Kebetulan, C dikenal sebagai 'Konstanta integrasi'.

Kami menulis ini sebagai:

∫ 3y².dx = y³ + C

Teknik integrasi untuk integral yang tidak terbatas, seperti pencarian tabel atau integrasi risch, dapat menambahkan diskontinuitas baru selama proses integrasi. Diskontinuitas baru ini muncul karena anti-turunan dapat memerlukan pengenalan logaritma kompleks.

Logaritma kompleks memiliki lompatan diskontinuitas ketika argumen melintasi sumbu nyata negatif, dan algoritma integrasi kadang -kadang tidak dapat menemukan representasi di mana lompatan ini dibatalkan.

Jika integral yang pasti dievaluasi dengan mencakup terlebih dahulu integral yang tidak terbatas dan kemudian mengganti batas integrasi ke dalam hasil, kita harus menyadari bahwa integrasi yang tidak terbatas dapat menghasilkan diskontinuitas. Jika ya, selain itu, kita harus menyelidiki diskontinuitas dalam interval integrasi.