Perbedaan antara codomain dan rentang

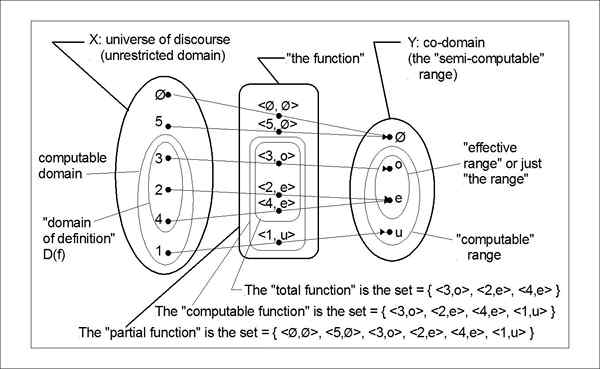
Baik codomain dan rentang adalah gagasan fungsi yang digunakan dalam matematika. Meskipun keduanya terkait dengan output, perbedaan antara keduanya cukup halus. Istilah "rentang" kadang -kadang digunakan untuk merujuk ke "codomain".  Saat Anda membedakan antara keduanya, maka Anda dapat merujuk ke codomain sebagai output fungsi dinyatakan untuk menghasilkan. Kisaran istilah, bagaimanapun, ambigu karena kadang -kadang dapat digunakan persis seperti codomain digunakan. Mari kita ambil F: A -> b, dimana F adalah fungsi dari a ke b. Kemudian, B adalah codomain dari fungsi "F”Dan rentang adalah himpunan nilai yang dilakukan fungsi, yang dilambangkan dengan F (A). Rentang bisa sama dengan atau kurang dari codomain tetapi tidak bisa lebih besar dari itu.

Misalnya, biarkan a = 1, 2, 3, 4, 5 dan b = 1, 4, 8, 16, 25, 64, 125. Fungsinya F: A -> b didefinisikan oleh F (x) = x ^3. Jadi disini,

Domain = mengatur a

Codomain = set b, dan

Range (r) = 1, 8, 64, 125

Kisaran harus menjadi kubus dari set A, tetapi kubus 3 (yaitu 27) tidak ada di set B, jadi kami memiliki 3 dalam domain, tetapi kami tidak memiliki 27 baik dalam codomain atau rentang. Kisarannya adalah subset dari codomain.

Apa itu codomain dari suatu fungsi?

"Codomain" dari suatu fungsi atau hubungan adalah seperangkat nilai yang mungkin keluar darinya. Ini sebenarnya adalah bagian dari definisi fungsi, tetapi membatasi output fungsi. Misalnya, mari kita ambil notasi fungsi F: R -> r. Itu artinya F adalah fungsi dari bilangan real ke bilangan real. Di sini, codomain adalah himpunan bilangan real r atau set output yang mungkin keluar darinya. Domain juga merupakan himpunan bilangan real r. Di sini, Anda juga dapat menentukan fungsi atau hubungan untuk membatasi nilai negatif yang dihasilkan oleh output. Secara sederhana, codomain adalah set di mana nilai fungsi jatuh.

Misalkan n menjadi himpunan bilangan alami dan hubungan didefinisikan sebagai r = (x, y): y = 2x, x, y ∈ N

Di sini, x dan y keduanya selalu merupakan bilangan alami. Jadi,

Domain = n, dan

Codomain = n itu adalah himpunan bilangan alami.

Apa rentang fungsi?

"Rentang" fungsi disebut sebagai himpunan nilai yang dihasilkan atau hanya sebagai set output nilainya. Kisaran istilah sering digunakan sebagai codomain, namun, dalam arti yang lebih luas, istilah ini dicadangkan untuk subset dari codomain. Secara sederhana, rentang adalah himpunan semua nilai output dari suatu fungsi dan fungsi adalah korespondensi antara domain dan rentang. Dalam teori set asli, rentang mengacu pada gambar fungsi atau codomain fungsi. Dalam matematika modern, rentang sering digunakan untuk merujuk pada gambar fungsi. Buku -buku yang lebih lama merujuk pada apa yang saat ini dikenal sebagai Codomain dan Buku Modern umumnya menggunakan rentang istilah untuk merujuk pada apa yang saat ini dikenal sebagai gambar. Sebagian besar buku tidak menggunakan rentang kata sama sekali untuk menghindari kebingungan sama sekali.

Misalnya, biarkan a = 1, 2, 3, 4 dan b = 1, 4, 9, 25, 64. Fungsinya F: A -> b didefinisikan oleh F (x) = x ^2. Jadi di sini, set A adalah domain dan set B adalah codomain, dan range = 1, 4, 9. Kisaran adalah kuadrat dari A yang ditentukan oleh fungsi, tetapi kuadrat 4, yaitu 16, tidak ada dalam codomain atau rentang.

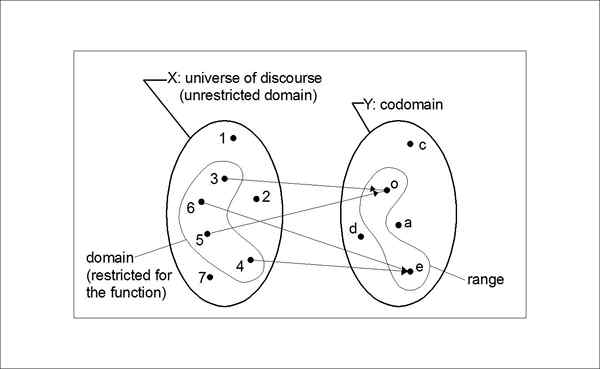
Perbedaan antara codomain dan rentang

Definisi codomain dan jangkauan

Kedua istilah tersebut terkait dengan output suatu fungsi, tetapi perbedaannya halus. Sementara codomain dari suatu fungsi adalah set nilai yang mungkin keluar darinya, itu sebenarnya bagian dari definisi fungsi, tetapi membatasi output fungsi. Kisaran suatu fungsi, di sisi lain, mengacu pada set nilai yang sebenarnya dihasilkannya.

Tujuan Codomain dan Range

Codomain dari suatu fungsi adalah serangkaian nilai yang mencakup rentang tetapi dapat mencakup beberapa nilai tambahan. Tujuan codomain adalah untuk membatasi output dari suatu fungsi. Kisaran ini bisa sulit untuk ditentukan kadang -kadang, tetapi set nilai yang lebih besar yang mencakup seluruh rentang dapat ditentukan. Codomain suatu fungsi terkadang memiliki tujuan yang sama dengan jangkauan.

Contoh codomain dan jangkauan

Jika a = 1, 2, 3, 4 dan b = 1, 2, 3, 4, 5, 6, 7, 8, 9 dan hubungannya F: A -> b didefinisikan oleh F (x) = x ^2, lalu codomain = set b = 1, 2, 3, 4, 5, 6, 7, 8, 9 dan range = 1, 4, 9. Kisarannya adalah kuadrat dari set A tetapi kuadrat 4 (yaitu 16) tidak ada di kedua set B (codomain) atau rentang.

Codomain vs. Rentang: Bagan Perbandingan

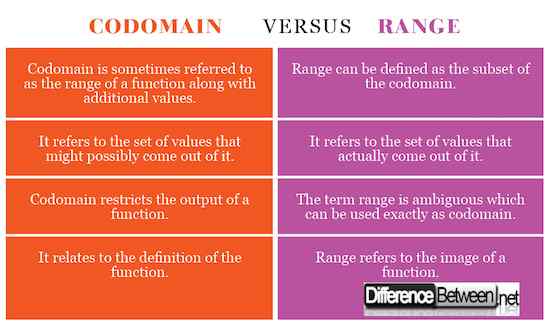
Ringkasan codomain vs. Jangkauan

Sementara keduanya adalah istilah umum yang digunakan dalam teori set asli, perbedaan antara keduanya cukup halus. Codomain dari suatu fungsi dapat dengan mudah disebut sebagai himpunan nilai output yang mungkin terjadi. Dalam istilah matematika, itu didefinisikan sebagai output dari suatu fungsi. Kisaran suatu fungsi, di sisi lain, dapat didefinisikan sebagai himpunan nilai yang benar -benar keluar darinya. Namun, istilah ini ambigu, yang berarti dapat digunakan kadang -kadang persis seperti codomain. Namun, dalam matematika modern, rentang digambarkan sebagai subset dari codomain, tetapi dalam arti yang jauh lebih luas.