Perbedaan antara distribusi binomial dan poisson

- 2908
- 746
- Bennie Herman
 Itu distribusi binomial adalah satu, yang kemungkinan jumlah hasilnya adalah dua, saya.e. keberhasilan atau kegagalan. Di sisi lain, tidak ada batasan hasil yang mungkin terjadi distribusi racun
Itu distribusi binomial adalah satu, yang kemungkinan jumlah hasilnya adalah dua, saya.e. keberhasilan atau kegagalan. Di sisi lain, tidak ada batasan hasil yang mungkin terjadi distribusi racun
Distribusi probabilitas teoritis didefinisikan sebagai fungsi yang memberikan probabilitas untuk setiap hasil yang mungkin dari percobaan statistik. Distribusi probabilitas dapat diskrit atau kontinu, di mana, dalam variabel acak diskrit, total probabilitas dialokasikan ke titik massa yang berbeda saat dalam variabel acak kontinu probabilitas didistribusikan pada berbagai interval kelas.
Distribusi binomial dan distribusi Poisson adalah dua distribusi probabilitas diskrit. Distribusi normal, distribusi siswa, distribusi chi-square, dan distribusi F adalah jenis variabel acak kontinu. Jadi, di sini kita membahas perbedaan antara distribusi binomial dan poisson. Lihat.
Konten: Distribusi Binomial vs Poisson Distribution
- Grafik perbandingan
- Definisi
- Perbedaan utama
- Kesimpulan
Grafik perbandingan
| Dasar untuk perbandingan | Distribusi binomial | Distribusi racun |
|---|---|---|
| Arti | Distribusi binomial adalah salah satu di mana probabilitas jumlah uji coba yang diulang dipelajari. | Distribusi Poisson memberikan penghitungan peristiwa independen terjadi secara acak dengan periode waktu tertentu. |
| Alam | Biparametrik | Uniparametrik |
| Jumlah uji coba | Tetap | Tak terbatas |
| Kesuksesan | Probabilitas konstan | Peluang kesuksesan yang sangat kecil |
| Hasil | Hanya dua hasil yang mungkin, saya.e. keberhasilan atau kegagalan. | Jumlah hasil yang tidak terbatas. |
| Mean dan Variance | Berarti> Varians | Rata -rata = varian |
| Contoh | Eksperimen melempar koin. | Mencetak kesalahan/halaman buku besar. |
Definisi distribusi binomial
Distribusi binomial adalah distribusi probabilitas yang banyak digunakan, berasal dari proses Bernoulli, (percobaan acak yang dinamai setelah matematikawan terkenal Bernoulli). Ini juga dikenal sebagai distribusi biparametrik, karena ditampilkan oleh dua parameter n dan p. Di sini, N adalah uji coba yang diulang dan P adalah probabilitas keberhasilan. Jika nilai dari kedua parameter ini diketahui, maka itu berarti bahwa distribusi diketahui sepenuhnya. Rata -rata dan varian distribusi binomial dilambangkan dengan µ = NP dan σ2 = NPQ.
P (x = x) = NCX PX Qn-x, x = 0,1,2,3 ... n
= 0, sebaliknya
Upaya untuk menghasilkan hasil tertentu, yang sama sekali tidak pasti dan tidak mungkin, disebut persidangan. Uji coba independen dan bilangan bulat positif tetap. Ini terkait dengan dua acara yang saling eksklusif dan lengkap; dimana kejadiannya disebut keberhasilan dan tidak terjadi kegagalan. P mewakili probabilitas keberhasilan sementara q = 1 - p mewakili probabilitas kegagalan, yang tidak berubah sepanjang proses.
Definisi Distribusi Poisson
Pada akhir 1830 -an, seorang matematikawan Prancis terkenal Simon Denis Poisson memperkenalkan distribusi ini. Ini menggambarkan probabilitas jumlah peristiwa tertentu yang terjadi dalam interval waktu yang tetap. Ini adalah distribusi uniparametrik karena hanya ditampilkan oleh satu parameter λ atau m. Dalam distribusi poisson rata -rata dilambangkan dengan m i.e. µ = m atau λ dan varians diberi label σ2 = m atau λ. Fungsi massa probabilitas X diwakili oleh:
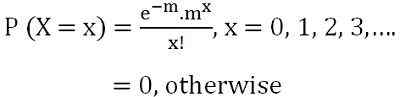 di mana e = kuantitas transendental, yang nilainya perkiraannya adalah 2.71828
di mana e = kuantitas transendental, yang nilainya perkiraannya adalah 2.71828
Ketika jumlah peristiwa tinggi tetapi probabilitas kejadiannya cukup rendah, distribusi Poisson diterapkan. Sebagai contoh, jumlah klaim/hari asuransi pada perusahaan asuransi.
Perbedaan utama antara distribusi binomial dan Poisson
Perbedaan antara distribusi binomial dan Poisson dapat ditarik dengan jelas dengan alasan berikut:
- Distribusi binomial adalah distribusi di mana probabilitas jumlah uji coba yang diulang dipelajari. Distribusi probabilitas yang memberikan penghitungan sejumlah peristiwa independen terjadi secara acak dalam periode tertentu, disebut distribusi probabilitas.
- Distribusi binomial adalah biparametrik, i.e. Ini ditampilkan oleh dua parameter n dan p sedangkan distribusi poisson uniparametrik, i.e. ditandai dengan satu parameter m.
- Ada sejumlah upaya dalam distribusi binomial. Di sisi lain, sejumlah uji coba tidak terbatas ada dalam distribusi Poisson.
- Probabilitas keberhasilan konstan dalam distribusi binomial tetapi dalam distribusi Poisson, ada sejumlah kecil peluang keberhasilan.
- Dalam distribusi binomial, hanya ada dua hasil yang mungkin, saya.e. keberhasilan atau kegagalan. Sebaliknya, ada sejumlah kemungkinan hasil yang tidak terbatas dalam kasus distribusi Poisson.
- Dalam distribusi binomial rata -rata> varian saat dalam distribusi poisson rata -rata = varian.
Kesimpulan
Terlepas dari perbedaan di atas, ada sejumlah aspek serupa antara kedua distribusi ini i.e. Keduanya adalah distribusi probabilitas teoritis diskrit. Lebih lanjut, berdasarkan nilai parameter, keduanya bisa unimodal atau bimodal. Selain itu, distribusi binomial dapat diperkirakan dengan distribusi Poisson, jika jumlah upaya (n) cenderung probabilitas tak terbatas dan keberhasilan (p) cenderung 0 sehingga m = np.
- « Perbedaan antara statistik dan parameter
- Perbedaan antara pengumpulan metode minat dan metode pembelian »

