Perbedaan antara persatuan dan persimpangan

Sebelum memahami perbedaan antara dua serikat pekerja yang ditetapkan dan persimpangan, mari kita pahami konsep teori yang ditetapkan terlebih dahulu. Teori yang ditetapkan adalah cabang mendasar dari matematika yang ditetapkan oleh studi, terutama apakah suatu objek milik, atau bukan milik, satu set objek yang entah bagaimana matematika yang relevan. Set pada dasarnya adalah kumpulan objek yang terdefinisi dengan baik, yang mungkin atau mungkin tidak memiliki relevansi matematika, seperti angka atau fungsi. Objek dalam satu set disebut elemen, yang bisa seperti angka, orang, mobil, negara bagian, dll. Hampir semua hal dan sejumlah elemen dapat dikumpulkan bersama untuk membuat set.

Secara sederhana, Set adalah kumpulan dari sejumlah elemen yang tidak berurutan yang dapat dianggap sebagai satu objek secara keseluruhan. Mari kita pahami konsep dasar dan notasi dari satu set dan bagaimana itu diwakili. Semuanya dimulai dengan hubungan biner antara objek X dan set a. Untuk mewakili jika x adalah anggota dari set A, notasi x ∊ a digunakan, sedangkan x ∉ a menunjukkan bahwa objek x tidak termasuk dalam himpunan a. Anggota satu set tercantum dalam kawat gigi keriting. Misalnya, himpunan bilangan prima kurang dari 10 dapat ditulis sebagai 2, 3, 5, 7. Demikian pula, satu set angka genap kurang dari 10 dapat ditulis sebagai 2, 4, 6, 8. Secara hipotetis, hampir semua set terbatas dapat diwakili oleh anggotanya.

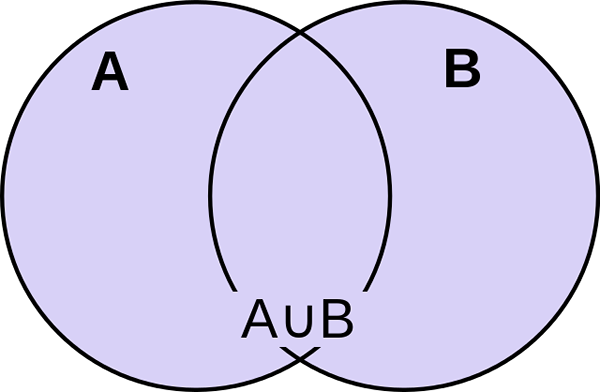
Apa itu persatuan set?

Persatuan dua set A dan B didefinisikan sebagai himpunan elemen yang termasuk dalam A atau B, atau mungkin keduanya. Itu hanya didefinisikan sebagai himpunan semua elemen atau anggota yang berbeda, di mana anggota termasuk salah satu dari set ini. Operator serikat sesuai dengan logis atau dan diwakili oleh simbol ∪. Itu adalah set terkecil yang berisi semua elemen dari kedua set. Misalnya, jika set a adalah 1, 2, 3, 4, 5 dan set b adalah 3, 4, 6, 7, 9, maka penyatuan a dan b diwakili oleh a∪b dan ditulis sebagai 1, 2, 3, 4, 5, 6, 7, 9. Karena angka 3 dan 4 hadir di kedua set A dan B, tidak perlu mencantumkannya dua kali. Jelaslah bahwa jumlah elemen penyatuan A dan B lebih kecil dari jumlah set individu, karena beberapa angka umum di kedua set.

A = 1, 3, 5, 7, 9

B = 3, 6, 9, 12, 15

A∪B = 1, 3, 5, 6, 7, 9, 12, 15

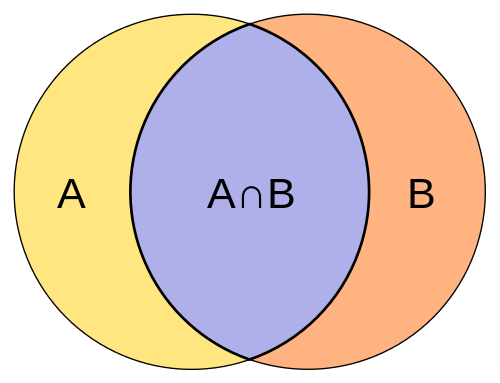
Apa persimpangan set?

Persimpangan dua set A dan B didefinisikan sebagai himpunan elemen milik A dan B. Ini hanya didefinisikan sebagai himpunan yang berisi semua elemen dari himpunan A yang juga termasuk dalam himpunan B, dan juga semua elemen set B milik set A. Operator persimpangan sesuai dengan logis dan dan diwakili oleh simbol ∩. Sebaliknya, persimpangan dua set adalah set terbesar yang berisi semua elemen yang umum untuk kedua set. Misalnya, jika set a adalah 1, 2, 3, 4, 5 dan set b adalah 3, 4, 6, 7, 9, lalu persimpangan a dan b diwakili oleh a∩b dan ditulis sebagai 3, 4. Karena hanya angka 3 dan 4 yang umum di kedua set A dan B, mereka disebut persimpangan set.

A = 2, 3, 5, 7, 11

B = 1, 3, 5, 7, 9, 11

A∩b = 3, 5, 7, 11

Perbedaan antara persatuan dan persimpangan set

1. Dasar - Persatuan dua set A dan B didefinisikan sebagai himpunan elemen yang termasuk dalam A atau B, atau mungkin keduanya, sedangkan persimpangan dua set didefinisikan sebagai himpunan elemen yang termasuk dalam A dan B baik.
2. Representasi simbolik - Persatuan dua set diwakili oleh simbol "∪", sedangkan persimpangan dua set diwakili oleh simbol "∩".
3. Relevansi logis - Persatuan dua set sesuai dengan logis "atau" sedangkan persimpangan dua set sesuai dengan logis "dan".
4. Contoh - Biarkan a = a, e, i, o, u dan

B = a, b, c, d, e, f

A∪b = a, b, c, d, e, f, i, o, u

A∩b = a, e

Union vs. Persimpangan: Bagan Perbandingan

Ringkasan Union VS. Persimpangan

Baik persatuan dan persimpangan adalah dua operasi mendasar yang melaluinya set dapat digabungkan dan terkait satu sama lain. Dalam hal teori yang ditetapkan, persatuan adalah himpunan semua elemen yang ada di kedua set, atau di keduanya, sedangkan persimpangan adalah himpunan semua elemen berbeda yang termasuk dalam kedua set tersebut. Persatuan dua set A dan B dilambangkan sebagai "A∪B", sedangkan persimpangan A dan B dilambangkan sebagai "A∩B". Set tidak lain adalah kumpulan objek yang terdefinisi dengan baik, seperti angka dan fungsi, dan objek dalam satu set disebut sebagai elemen.