Perbedaan antara standar deviasi dan kesalahan standar
- 3516
- 184
- Mr. Doug Effertz
Deviasi standar didefinisikan sebagai ukuran absolut dispersi dari suatu seri. Itu mengklarifikasi jumlah standar variasi di kedua sisi rata -rata. Ini sering disalahartikan dengan kesalahan standar, karena didasarkan pada standar deviasi dan ukuran sampel.
Kesalahan standar digunakan untuk mengukur akurasi statistik suatu perkiraan. Ini terutama digunakan dalam proses pengujian hipotesis dan memperkirakan interval.
Ini adalah dua konsep penting statistik, yang banyak digunakan di bidang penelitian. Perbedaan antara standar deviasi dan kesalahan standar didasarkan pada perbedaan antara deskripsi data dan inferensi -nya.
Konten: Deviasi Standar vs Kesalahan Standar
- Grafik perbandingan
- Definisi
- Perbedaan utama
- Kesimpulan
Grafik perbandingan
| Dasar untuk perbandingan | Deviasi standar | Kesalahan standar |
|---|---|---|
| Arti | Deviasi standar menyiratkan ukuran dispersi set nilai dari rata -rata. | Kesalahan standar berkonotasi ukuran ketepatan statistik suatu perkiraan. |
| Statistik | Deskriptif | Inferensial |
| Pengukuran | Berapa banyak pengamatan bervariasi satu sama lain. | Seberapa tepat sampel berarti berarti populasi yang sebenarnya. |
| Distribusi | Distribusi pengamatan tentang kurva normal. | Distribusi perkiraan tentang kurva normal. |
| Rumus | Akar varians kuadrat | Deviasi standar dibagi dengan akar kuadrat ukuran sampel. |
| Peningkatan ukuran sampel | Memberikan ukuran standar deviasi yang lebih spesifik. | Mengurangi kesalahan standar. |
Definisi standar deviasi
Standar deviasi, adalah ukuran penyebaran seri atau jarak dari standar. Pada tahun 1893, Karl Pearson menciptakan gagasan standar deviasi, yang tidak diragukan lagi merupakan ukuran yang paling digunakan, dalam studi penelitian.
Itu adalah akar kuadrat dari rata -rata kotak penyimpangan dari rata -rata mereka. Dengan kata lain, untuk kumpulan data yang diberikan, standar deviasi adalah deviasi root-mean-square, dari rata-rata aritmatika. Untuk seluruh populasi, itu ditunjukkan oleh surat Yunani 'sigma (σ)', dan untuk sampel, itu diwakili oleh huruf Latin 's'.
Deviasi standar adalah ukuran yang mengukur tingkat dispersi set pengamatan. Semakin jauh titik data dari nilai rata -rata, semakin besar deviasi dalam set data, menyatakan bahwa titik data tersebar di rentang nilai yang lebih luas dan sebaliknya.
- Untuk data yang tidak diklasifikasi:
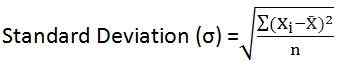
- Untuk distribusi frekuensi yang dikelompokkan:
Definisi kesalahan standar
Anda mungkin telah mengamati bahwa sampel yang berbeda, dengan ukuran yang identik, diambil dari populasi yang sama, akan memberikan beragam nilai statistik yang sedang dipertimbangkan, i.e. rata -rata sampel. Standard ERROR (SE) memberikan, standar deviasi dalam nilai rata -rata sampel yang berbeda. Itu digunakan untuk membuat perbandingan antara sarana sampel di seluruh populasi.
Singkatnya, kesalahan standar statistik tidak lain adalah standar deviasi dari distribusi pengambilan sampelnya. Ini memiliki peran besar untuk memainkan pengujian hipotesis statistik dan estimasi interval. Itu memberikan gambaran tentang ketepatan dan keandalan perkiraan. Semakin kecil kesalahan standar, semakin besar keseragaman distribusi teoritis dan sebaliknya.
- Rumus: Kesalahan standar untuk rata -rata sampel = σ/√n
Dimana, σ adalah standar deviasi populasi
Perbedaan utama antara standar deviasi dan kesalahan standar
Poin -poin yang dinyatakan di bawah ini substansial sejauh perbedaan antara standar deviasi yang bersangkutan:
- Standar deviasi adalah ukuran yang menilai jumlah variasi dalam rangkaian pengamatan. Kesalahan standar mengukur keakuratan suatu perkiraan, i.e. Ini adalah ukuran variabilitas distribusi teoritis statistik.
- Deviasi Standar adalah statistik deskriptif, sedangkan kesalahan standar adalah statistik inferensial.
- Standar Deviasi mengukur seberapa jauh nilai individu dari nilai rata -rata. Sebaliknya, seberapa dekat rata -rata sampel dengan rata -rata populasi.
- Deviasi standar adalah distribusi pengamatan dengan mengacu pada kurva normal. Berlawanan dengan ini, kesalahan standar adalah distribusi estimasi dengan mengacu pada kurva normal.
- Deviasi standar didefinisikan sebagai akar kuadrat dari varians. Sebaliknya, kesalahan standar digambarkan sebagai standar deviasi dibagi dengan akar kuadrat dari ukuran sampel.
- Saat ukuran sampel dinaikkan, ia memberikan ukuran standar deviasi yang lebih khusus. Tidak seperti, kesalahan standar saat ukuran sampel meningkat, kesalahan standar cenderung berkurang.
Kesimpulan
Pada umumnya, standar deviasi dianggap sebagai salah satu ukuran dispersi terbaik, yang mengukur dispersi nilai dari nilai pusat. Di sisi lain, kesalahan standar terutama digunakan untuk memeriksa keandalan dan keakuratan estimasi dan karenanya, semakin kecil kesalahannya, semakin besar keandalan dan keakuratannya.