Perbedaan antara bilangan real dan bilangan bulat

Matematikawan telah mengembangkan sistem untuk menentukan bagaimana angka tertentu berbeda dari yang lain. Sama seperti konsep lainnya, kategori angka tumpang tindih. Karena bilangan real mencakup semua bilangan rasional seperti bilangan bulat, mereka memiliki karakteristik yang sama seperti pemanfaatan bilangan bulat dan diplot pada garis angka. Oleh karena itu, perbedaan utama adalah bahwa bilangan real adalah klasifikasi umum sementara bilangan bulat adalah subset yang ditandai sebagai bilangan bulat yang dapat memiliki sifat negatif.

Apa bilangan real?

Bilangan real adalah nilai yang dapat Anda temukan pada garis angka yang biasanya dinyatakan sebagai garis horizontal geometris di mana titik yang dipilih berfungsi sebagai "asal". Mereka yang jatuh di sisi kanan diberi label positif sementara yang di sebelah kiri negatif. Deskripsi "nyata" disajikan oleh Rene Descartes, seorang ahli matematika dan filsuf terkenal di abad ke -17. Dia secara khusus menetapkan perbedaan antara akar nyata polinomial dan akar imajiner mereka.

Bilangan real termasuk bilangan bulat utuh, bilangan bulat, alami, rasional, dan irasional:

• Bilangan bulat

Bilangan bulat adalah bilangan positif yang tidak memiliki bagian fraksional atau titik desimal karena mereka mewakili seluruh objek tanpa fragmen atau potongan.

• Bilangan bulat

Bilangan bulat adalah bilangan bulat yang mencakup sisi negatif dari garis angka.

• Bilangan alami

Juga dikenal sebagai penghitungan angka, bilangan alami seperti bilangan bulat tetapi nol tidak termasuk karena tidak ada yang bisa dihitung sebagai "0".

• Angka rasional

Mengenai asal -usulnya, Pythagoras, ahli matematika Yunani kuno menyatakan bahwa semua angka itu rasional. Bilangan rasional adalah quotient atau fraksi dua bilangan bulat.  Di mana P dan Q adalah bilangan bulat dan Q tidak setara dengan nol, p/q adalah bilangan rasional. Misalnya, 3/5 adalah bilangan rasional tetapi 3/0 tidak.

• Bilangan irasional

Siswa Pythagoras, Hippasus tidak setuju bahwa semua angka rasional. Melalui geometri, ia membuktikan bahwa beberapa bilangan itu tidak rasional. Misalnya, akar kuadrat dari dua, yaitu 1.41 tidak dapat dinyatakan sebagai fraksi; Oleh karena itu, tidak rasional. Sayangnya, aktualitas bilangan rasional tidak diterima oleh pengikut Pythagoras. Ini mengakibatkan Hippasus tenggelam di laut yang dikatakan sebagai hukuman dari para dewa selama waktu itu.

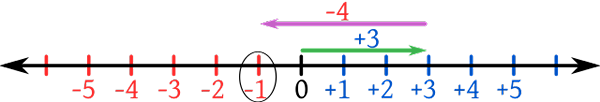
Apa itu bilangan bulat?

Dari kata Latin "integer", yang diterjemahkan menjadi "keseluruhan" atau "tidak tersentuh", angka -angka ini tidak memiliki komponen fraksional atau desimal seperti halnya bilangan bulat. Angka -angka tersebut termasuk angka alami yang positif atau angka penghitungan dan negatifnya. Misalnya, -3, -2, -1, 0, -1, 2, 3 adalah bilangan bulat. Ilustrasi biasa adalah bilangan spasi yang sama pada garis bilangan tak terbatas dengan nol, yang tidak positif atau negatif, di tengah. Oleh karena itu, positifnya lebih besar dari yang negatif.

Mengenai sejarahnya, akun -akun berikut melacak bagaimana bilangan bulat pertama kali digunakan:

• Di 200 b.C. Angka negatif pertama kali diwakili dengan batang merah di Cina kuno.
• Di sekitar 630 a.D., Angka negatif digunakan untuk mewakili utang di India.
• Arbermouth Holst, ahli matematika Jerman memperkenalkan bilangan bulat pada tahun 1563 sebagai sistem sebagai tambahan dan perkalian. Dia mengembangkan sistem sebagai respons terhadap meningkatnya jumlah kelinci dan gajah yang dia coba.

Berikut ini adalah karakteristik bilangan bulat:

• Positif

Angka -angka di sisi kanan garis angka positif dan mereka sering mewakili nilai yang lebih tinggi dari rekan -rekan negatif mereka.

• Negatif

Angka -angka di sisi kiri garis angka sering dipandang sebagai nilai standar yang lebih rendah dari rekan -rekan positif mereka.

• Netral

Pusat garis angka, nol adalah bilangan bulat yang tidak positif atau negatif.

• Tidak ada fragmen

Seperti bilangan bulat, bilangan bulat tidak memiliki titik desimal atau pecahan.

Perbedaan antara bilangan real dan bilangan bulat

Ruang lingkup bilangan real dan bilangan bulat

Bilangan real termasuk bilangan bulat, rasional, irasional, alami, dan bilangan bulat. Di sisi lain, ruang lingkup bilangan bulat terutama berkaitan dengan bilangan bulat yang negatif dan positif. Oleh karena itu, bilangan real lebih umum.

Pecahan

Bilangan real dapat mencakup pecahan seperti bilangan rasional dan irasional. Namun, pecahan tidak bisa menjadi bilangan bulat.

Properti terkecil di atas

Bilangan real memiliki property paling tidak-atas yang juga dikenal sebagai "kelengkapan". Ini berarti bahwa set linear bilangan real memiliki himpunan bagian dengan kualitas supremum.  Sebaliknya, bilangan bulat tidak memiliki properti yang paling sedikit di atas.

Properti Archimedean

Properti Archimedean, yang merupakan asumsi bahwa ada angka alami yang sama dengan atau lebih besar dari bilangan real apa pun, dapat diterapkan pada bilangan real. Sebaliknya, properti Archimedean tidak dapat diterapkan pada bilangan bulat.

Bidang

Bilangan real adalah sejenis bidang yang merupakan struktur aljabar penting di mana proses aritmatika didefinisikan. Sebaliknya, bilangan bulat tidak dianggap sebagai bidang.

Dapat dihitung

Sebagai satu set, bilangan real tidak terhitung saat bilangan bulat dihitung.

Simbol bilangan real dan bilangan bulat

Bilangan real dilambangkan sebagai "r" sementara satu set bilangan bulat dilambangkan sebagai "z".  N. Bourbaki, sekelompok ahli matematika Prancis pada 1930 -an, ditentukan "z" dari kata Jerman "Zahlen" yang berarti jumlah atau bilangan bulat.

Asal kata untuk bilangan real dan bilangan bulat

Bilangan real menunjukkan akar nyata dari polinomial sementara Integer berasal dari kata Latin, "utuh" karena mereka tidak termasuk desimal atau pecahan.

Bilangan real vs bilangan bulat

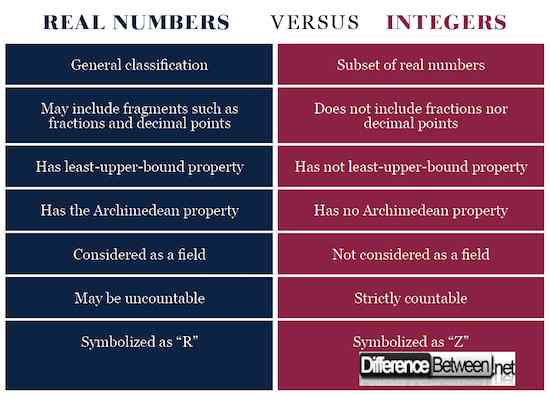
Ringkasan bilangan real vs.  Bilangan bulat

• Baik bilangan real dan bilangan bulat dapat diplot pada baris angka.
• Bilangan bulat adalah subset dari bilangan real.
• Bilangan bulat memiliki angka negatif.
• Sebagai satu set, bilangan real memiliki ruang lingkup yang lebih umum dibandingkan dengan bilangan bulat.
• Tidak seperti bilangan bulat, bilangan real mungkin termasuk pecahan dan titik desimal.
• Properti yang paling tidak terikat, Archimedean, dan bidang umumnya berlaku untuk bilangan real tetapi tidak untuk bilangan bulat.
• Tidak seperti bilangan real, bilangan bulat dapat dihitung secara ketat.
• "R" adalah singkatan dari bilangan real saat "z" adalah untuk bilangan bulat.