Perbedaan antara komutatif dan asosiatif

Matematika adalah permainan angka dan angka ada di mana -mana. Dan aturan permainan adalah properti dan aturan yang terkait dengan angka. Properti membantu Anda menghitung jawaban di kepala Anda dengan cepat dan mudah. Properti tidak lain adalah aturan khusus yang diikuti angka. Ada tiga sifat dasar angka yang menurut setiap sistem matematika: sifat komutatif, asosiatif, dan distributif. Properti ini adalah fitur dari empat operasi (tambahkan, kurangi, melipatgandakan, dan membagi) yang selalu berlaku terlepas dari nomor yang Anda kerjakan. Tapi kami hanya akan membahas sifat komutatif dan asosiatif dalam artikel berikut.

Baik properti komutatif maupun asosiatif adalah aturan yang diterapkan pada operasi penambahan dan perkalian. Properti ini adalah undang -undang yang digunakan dalam aljabar untuk membantu memecahkan masalah. Properti komutatif berasal dari istilah "perjalanan" yang berarti bergerak dan mengacu pada dapat mengubah angka yang Anda tambahkan atau kembangkan. Properti asosiatif berasal dari kata "rekan" atau "grup" dan itu mengacu pada pengelompokan tiga angka atau lebih menggunakan tanda kurung, terlepas dari bagaimana Anda mengelompokkannya. Hasilnya tetap sama, tidak peduli bagaimana Anda mengelompokkan kembali angka-angkanya. Mari kita lihat dua properti untuk lebih memahami cara kerjanya.

Apa yang komutatif?

Misalnya; Kami tahu bahwa menambahkan 2 dan 5 memberikan jawaban yang sama dengan menambahkan 5 dan 2. Urutan angka dalam masalah penambahan dapat diubah tanpa mengubah hasilnya. Hal ini tentang angka dan penambahan disebut properti komutatif penambahan. Jadi, kita bisa mengatakan penambahan adalah operasi komutatif. Demikian pula, perkalian adalah operasi komutatif.

Properti Komutatif Penambahan:

a + b = b + a

3 + 4 = 7 sama dengan 4 + 3 = 7

Hasilnya akan sama terlepas dari urutan angka.

Properti Komutatif Perkalian:

A × B = B × A

3 × 7 = 21 sama dengan 7 × 3 = 21

Demikian juga, hasilnya akan sama terlepas dari urutan angka.

Apa itu asosiatif?

Asosiatif adalah properti lain yang kami gunakan berkaitan dengan mengelompokkan kembali. Misalnya, saat menambahkan 2 + 3 + 5, kita dapat menambahkan 2 dan 3 terlebih dahulu dan kemudian menambahkan 5, atau kita dapat menambahkan 3 dan 5 pertama dan kemudian 2. Secara matematis, sepertinya ini: 2 + 3 + 5 = 2 + (3 + 5) = (2 +3) + 5. Operasi yang berperilaku dengan cara ini disebut operasi asosiatif. Hasilnya tetap sama bahkan jika kita mengubah pengelompokan angka.

Properti Asosiatif Penambahan:

A + (B + C) = (A + B) + C = A + B + C

1 + (2 +3) = (1 +2) + 3 = 6

Hasilnya tetap sama, tidak peduli bagaimana Anda mengelompokkan angkanya.

Properti asosiatif dari perkalian:

A × (B × C) = (A × B) × C

2 × (3 × 4) = 2 × 12 = 24

(2 × 3) × 4 = 6 × 4 = 24

Jadi, pengelompokan dalam angka tidak mengubah hasilnya.

Perbedaan antara komutatif dan asosiatif

Arti

- Properti komutatif berasal dari istilah "perjalanan" yang berarti 'bergerak' dan mengacu pada dapat mengubah angka yang Anda tambahkan atau kelipat terlepas dari urutan angka -angka tersebut. Properti asosiatif, di sisi lain, berasal dari kata "associate" atau "grup" dan mengacu pada pengelompokan tiga angka atau lebih menggunakan tanda kurung, terlepas dari bagaimana Anda mengelompokkannya. Hasilnya akan sama, tidak peduli bagaimana Anda mengelompokkan kembali angka atau variabel.

Aturan

- Aturan komutatif negara penambahan, a + b = b + a, yang berarti menambahkan a dan b memberikan hasil yang sama dengan menambahkan b dan a. Pesanan dapat berubah tanpa mengubah hasilnya. Aturan penambahan ini disebut properti komutatif penambahan. Demikian pula, perkalian adalah operasi komutatif yang berarti A × B akan memberikan hasil yang sama dengan B × A. Properti asosiatif, di sisi lain, adalah aturan yang mengacu pada pengelompokan angka. Aturan asosiatif status penambahan, a + (b + c) sama dengan (a + b) + c. Demikian juga, aturan asosiatif perkalian mengatakan a × (b × c) sama dengan (a × b) × c.

Contoh

- Properti Komutatif Penambahan: 1 + 2 = 2 +1 = 3

Properti Komutatif Perkalian: 2 × 3 = 3 × 2 = 6

Properti asosiatif penambahan: 5 + (3 + 7) = (5 + 3) + 7 = 15

Properti asosiatif perkalian: 5 × (2 × 4) = (5 × 2) × 4 = 40

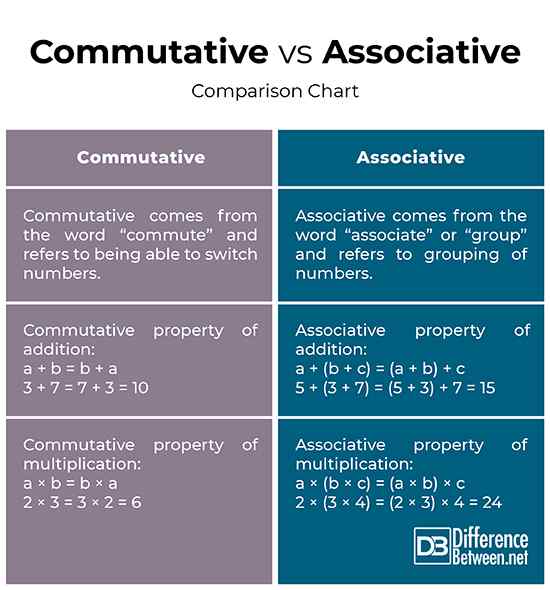
Komutatif vs. Asosiatif: Bagan Perbandingan

Ringkasan

Singkatnya, properti komutatif tidak membingungkan dengan properti asosiatif. Properti komutatif menyatakan bahwa tidak apa -apa untuk mengubah urutan angka selain operasi penggandaan karena hasilnya akan sama, tidak peduli pesanannya. Properti asosiatif, di sisi lain, menyatakan bahwa hasilnya akan sama, tidak peduli bagaimana Anda mengelompokkan jumlah atau variabel dalam operasi tambahan/multiplikasi.